It occurred to me that the Self-Attention calculation that forms the core of Transformers in LLMs such as ChatGPT, can be understood as an offshoot of the autocorrelation calculations that one often sees in traditional science and engineering. Basically, to understand the relationship between a time series with itself at various points in time, one can shift the sequence by various intervals and calculate the cross correlation with itself i.e. the inner product of the sequence with its shifted counterpart (see equation 7 from Wikipedia below). Higher values of the auto-correlation imply similarity or high correlation of the sequence with itself at the time implied by the shift.
Self-Attention calculations are doing something similar in a more generalized and layered form. Rather than directly taking the inner product of the sequence with its shifted form, Transformers map the input data sequence into an alternate form (represented by Queries, Keys and Values) which are then aggregated in a way that is ultimately an inner product as well (see lower right equation in Wikipedia diagram below). In essence, rather than taking
x*x_shift we take
f(x)*g(x) where f and g involve matrix multiplications with learned weights as well as a SoftMax function. Both Self-Attention and auto-correlation can be understood then as special cases of a generalized self-correlation calculation for particular forms of the mappings f and g. For example, in auto-correlation f is simply the identity and g is a time-shift.
References:
Autocorrelation - Wikipedia
Attention (machine learning) - Wikipedia
Cross-correlation - Wikipedia
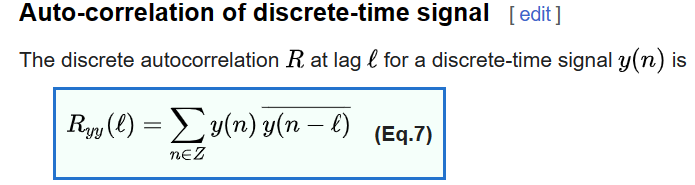



Comments
Post a Comment