Notes on Embedding Models: From Architecture to Implementation

I recently completed DeepLearning.AI's interesting short course on Embedding Models (Embedding Models: from Architecture to Implementation - DeepLearning.AI). In essence, the course covers how embeddings are used in ML to convert disparate forms of data e.g. text and images into numerical representations as vectors, with particular emphasis on linguistic text data. One idea I had from the course is that multimodal models may take advantage of embeddings since images and text can be converted into vector (or perhaps generalized matrix/tensor form) such that the resulting objects can undergo operations together in a compatible manner so as to enable multimodal generative AI e.g. producing images from text inputs. Presumably, this is how something like Gemini or ChatGPT produces images from user inputted text. It appears that OpenAI's early multimodal model CLIP (Contrastive Language-Image Pretraining) utilizes such an approach by mapping text and images into the same mathematical space. Vertex AI in Google Cloud looks to be using a similar approach as well quoting from the documentation: "the same semantic space with the same dimensionality. Consequently, these vectors can be used interchangeably for use cases like searching image by text or searching video by image."

Below are my rough notes from the course:

- Vector embeddings map real world entities to points in vector space.

- word2vec was the original fundamental model for mapping words to vectors

- Embeddings permit intuitive "semantic algebra" with intuitive interpretation as shown below where the vector algebra between the embeddings of "Yoda", "good" and "evil" produces "Vader".

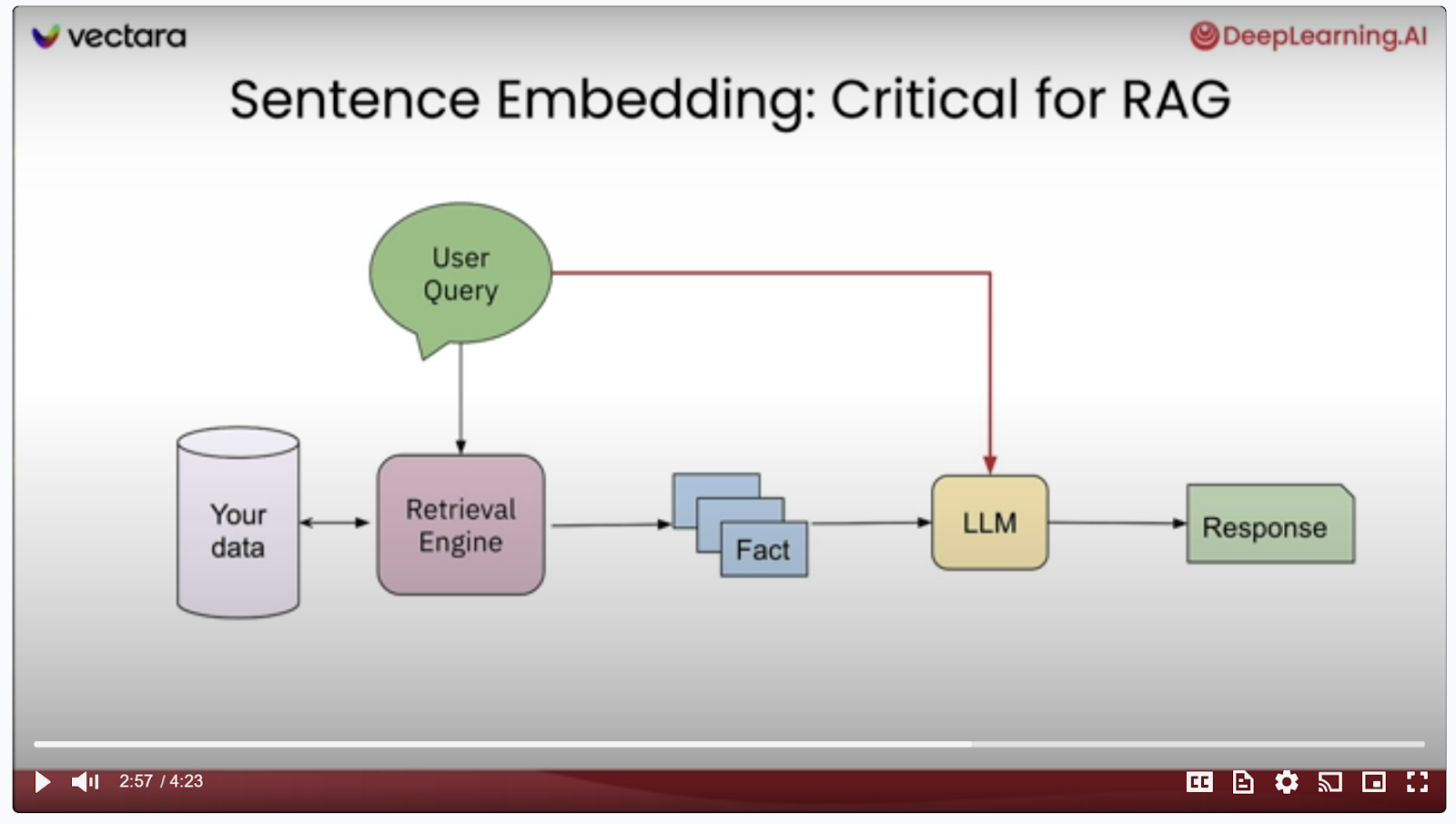
- Embeddings are generally applicable to different types of data, which ultimately enables multimodal models to function and process disparate data types (think Gemini or ChatGPT produces images from user text inputs).






- Bert was one of the first Transformer-based LLMs to gain traction. Interestingly, it was trained on ~10x as many words as it has parameters. This is nice to see, as I have always said it is a good rule of thumb to train ML models on data that is at least 1 order of magnitude (10x) bigger than the model.


- Great example of PCA to bring the 100-dimensional word embedding vectors into a much more visually tractable 2D form




-Word2Vec embeddings do not preserve information about context when embedding words to vectors
- Transformers on the other hand are able to preserve context in the embeddings e.g. "bat" as an animal versus "bat" as a sporting good depending on the sentence. This makes sense since Transformers utilize Attention mechanisms in order to capture long-distance correlations across sequences of data (see post on "Transformers as Autocorrelations"). The Decoder piece of the Transformer architecture does so by processing and effectively integrating information across word embeddings from the Encoder, that is they attend to word tokens to the left and right of individual words in addition to the words themselves.







- Q: what is the difference between encoders and embeddings? Are encoders transformations that produce embeddings, or use embeddings or is the relationship different? The chain of logic appears to be tokenization -> encoding -> embedding. The below code sample shows succinctly that the spirit of the encoder is really to implement the conversion of the sentence into vector form. In this particular example, the embedding vectors are 768-dimensional. The embeddings appear to be implemented in a context-aware manner via the transformer encoder architecture (attention mechanisms in an autocorrelation manner). I think the right way to think about things is that encoders are a general notion for the initial layers of an LLM and they typically include transformations that produce embeddings.



- It is evident from sample histograms of the embedding vectors for the question and answer sentences above that the elements are typically in the range of -1 to 1, but not strictly so. One would except some kind of normalized range as is often the case in numerical recipes and mathematical models.


- Ultimately, embeddings are used full-circle in RAG pipelines, since the text data of the relevant documents the LLM can search through must be put into numerical form for internal processing e.g. similarity calculations based on the user query.




References:









 


Comments

Post a Comment

Popular Posts